Una manera de aumentar la eficiencia en la verificación de grandes cantidades de datos consiste en convertirlos de alguna manera en una forma resumida, que al mismo tiempo conserve la integridad y confiabilidad de los datos originales. Esta es la tarea de las funciones de hash, o el proceso de hashing, que también es llamado transformación de claves (Hash significa moler, o picar, digerir).
En el hashing, la función recibe como entrada datos de longitud variable, la salida producida será una cadena de caracteres alfanuméricos de longitud fija. No importa si la entrada es un saludo como “¡Hola, mundo!”, o el contenido de la biblioteca de leyes de Yale y Stanford juntas, las claves resultantes serán de idéntica extensión. Por supuesto, en el campo de las criptomonedas, la entrada para una función hash también puede ser el contenido de un bloque o una blockchain entera.
Seguridad de datos y hashes
Para que una función hash sea considerada segura y se la pueda utilizar confiadamente en el mundo de la criptografía, debe cumplir con varias características:
– Para cada entrada distinta debe producir un valor único. Esto ayuda a que las entradas puedan validarse como auténticas.
– Una entrada siempre dará como resultado la misma salida o valor. La autenticidad se pone a prueba nuevamente con esta propiedad.
– La función debe producir un resultado rápidamente, no importando el tamaño de los datos de entrada. Esto garantiza la eficacia de la misma.
– Debe ser irreversible. Basándose en el hash obtenido, no podrá obtenerse por ningún medio el conjunto de datos de entrada con lo originó. Aquí radica gran parte de la seguridad proveniente de las funciones hash, y son una de sus características más importantes.
– Un cambio ínfimo en los datos de entrada, deben producir un hash completamente distinto al obtenido cuando se procesa el conjunto original. La variación en el hash de salida tiene relación directa con la complejidad del algoritmo de la función.
El hash actúa como una firma que autentifica la integridad de los datos que se envían por un medio naturalmente inseguro como Internet. Para un conjunto de datos dados se calcula su hash, y el resultado se incluye en el paquete de envío. En el otro extremo de la operación, el receptor calcula de nuevo el hash y lo compara con el resultado obtenido por el emisor. Para que la información se tome como íntegra, sin alteraciones, ambos hashes deben ser idénticos.
Tipos de funciones hash
Para que podamos entender las funciones hash un poco mejor, debemos hablar antes de los números binarios. A fin de cuentas, indirectamente estamos haciendo referencia a ellos cada vez que mencionamos programas, claves, cadenas de bloques y criptomonedas. Todas las entidades que funcionan en y se transmiten por medios digitales se reducen a números binarios, es decir, bits y bytes.
Unos encendidos, otros apagados
Un bit es un dígito binario (binary digit), y toma dos valores: cero y uno. Un byte es un conjunto de ocho bits con el que se pueden representar datos digitalmente. En un byte, cada bit es como una casilla que tiene como valor asociado una potencia del número 2, asignados de izquierda a derecha:
1 byte = 128 – 64 – 32 – 16 – 8 – 4 – 2 – 1
Cuando una casilla del byte está ocupada por un bit “1” (encendido), el valor de la casilla (la potencia de 2) interviene en el cálculo del valor total de byte, cuando es “0” (apagado) el valor se ignora. De modo que si tenemos un byte compuesto de esta forma:
0 – 0 – 0 – 1 – 0 – 1 – 0 – 1
Sumaremos solamente los valores 16, 4 y 1, lo que nos da el valor del byte en este caso: 21. Con un byte, el mayor número que podemos representar es 256. Mientras más grande sea el número que necesitemos utilizar, hará falta una mayor cantidad de bits.

Cada vez que accedemos a un sitio en la web, estamos utilizando un número binario. La dirección IP (Protocolo de Internet) es un número de 32 bits que se asigna como identificador único de cada página que visitamos. Igualmente, para poder navegar en la red, nuestro equipo necesita de un identificador similar.
Las direcciones de la versión 4 de IP tienen el siguiente formato: 192.168.64.11, donde cada byte, aquí llamados octetos, está separado del siguiente por un punto.
SHA 256
SHA son las iniciales de Secure Hash Algorithm (algoritmo de hash seguro) y 256 es el número de su especificación en bits (equivalente a 32 bytes). La función hash SHA-256 forma parte de una serie de funciones, la primera de las cuales (SHA-0) fue publicada en 1993 por el Instituto Nacional de Estándares y Tecnología de los Estados Unidos. En 1995 se postuló SHA-1 y posteriormente, en 2001, salieron funciones hash de mayor grado de complejidad, conocidas en conjunto como funciones SHA-2. Las otras son: SHA-224, SHA-384, y SHA-512.
El hash producido por SHA-256 es una cadena compuesta por 64 dígitos hexadecimales como la siguiente:
fed27a05bdbfde723fccc5169959bf16340fdd9d4d91abd04143d266a059bce1
En blockchain, la función SHA-256 se emplea para garantizar la integridad de los registros incluidos en los bloques, en la creación de direcciones (envío y recepción de monedas) y como parte de la prueba de trabajo en el funcionamiento de la red Bitcoin. Los mineros obtienen una recompensa cuando encuentran un hash en particular que los habilita para incluir determinado bloque en la cadena. Para obtener dicho hash, deben manipular el campo nonce del bloque hasta dar con el valor hash requerido.
Funciones hash en las cadenas de bloques
Con el uso de funciones hash, es posible determinar en cualquier momento el estado de una cadena en blockchain. El conjunto de transacciones ya registradas, más las recién agregadas, se toma como la entrada de la función, que produce entonces la “imagen criptográfica” de todos los eventos de la red hasta ese punto.
Dado que el menor cambio en el conjunto de datos de entrada debe arrojar un hash totalmente diferente al de los datos originales, no es posible modificar los registros de un bloque sin afectar a todos los hashes derivados. Además, todos los demás nodos de la red deberán ponerse de acuerdo en que los nuevos hashes son válidos, lo que en ambientes descentralizados como blockchain no es posible debido a la naturaleza de su funcionamiento.
El bloque de génesis, el primero de una cadena, produce un hash que se usa como entrada para calcular el hash del siguiente bloque, junto a todas las transacciones registradas por éste. Aquí vemos que cada bloque está ligado al anterior por el valor hash, con la excepción del primer bloque generado. De esta forma se va creando una cadena de que conduce de vuelta hasta el bloque génesis, de donde nace el nombre “cadena de bloques”. Esto hace posible ir agregando los bloques en secuencia, “sellándolos” con un hash único, siempre y cuando los nodos participantes convengan en que sus valores son legítimos.
Estructuras de datos: listas vinculadas
Desde del punto de vista computacional, las cadenas de bloques son estructuras de datos conocidas como listas vinculadas, que son una forma de almacenamiento de datos donde cada elemento de la lista (bloque) se enlaza a otro (el bloque previo) usando una variable (hash) como puntero. Es en los punteros formados por hashes donde está la principal fortaleza de la tecnología blockchain en cuanto a integridad de datos. Además de contener la dirección del bloque anterior, un puntero también contiene el hash producto de los registros de ese bloque, y no es posible cambiar un hash sin afectar el resto de la cadena.

Las listas vinculadas se caracterizan por:
– Un acceso costoso a los datos
– El costo de añadir y eliminar información es alto (excepto en los extremos)
– El tamaño de la estructura es ilimitado
Como se indica, el empleo de listas vinculadas para el almacenamiento de datos es costoso e ineficiente, pues la creación de hashes implica cálculos que consumen tiempo y energía; el acceso a los datos y su verificación, a diferencia de otras estructuras, carece de agilidad. Es aquí donde interviene el árbol de Merkle en las cadenas de bloques.
Árboles de Merkle
El árbol de hashes, o árbol de Merkle, es una invención de Ralph Merkle, quien ideó esta estructura de datos mientras estudiaba para un título de computación en la Universidad de California – Berkeley en 1974. Merkle tuvo que esperar hasta 1976, cuando entró a la Universidad de Stanford, donde trabajo con los pioneros de la criptografía de clave pública Martin Hellman y Whitfield Diffie para desarrollar su descubrimiento.
La estructura está formada por un árbol invertido de hashes, con un hash raíz en la parte superior, del cual parten nodos-rama hacia abajo, que contienen hashes de otros nodos-rama de niveles inferiores, hasta llegar a las “hojas” del árbol, que en el caso de una cadena de bloques representan los eventos o transacciones.
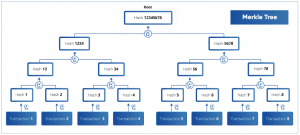
El árbol de Merkle es el producto un algoritmo que toma como datos de entrada el conjunto de transacciones almacenadas en un bloque con el fin de verificar que las mismas no hayan sido alteradas. El bloque no se procesa como un todo, sino que cada transacción es evaluada por separado, mientras el algoritmo las agrupa en segmentos vinculados, produciendo al final un hash del bloque completo.
Los arboles de Merkle permiten la representación arbitraria de conjuntos de datos de tamaño considerable, e identificar de manera eficiente si los mismos han sido comprometidos y qué parte de su estructura ha sido afectada, sin tener que procesarlos todos. Esto es posible utilizando las llamadas pruebas de Merkle.
Para aplicar una prueba de Merkle sólo hace falta conocer el hash raíz del grupo de datos que se quiere analizar. Siempre que esta raíz sea confiable, tanto la posición como la integridad de un dato perteneciente a un determinado conjunto pueden ser verificadas, estudiando solamente la rama del árbol asociada al dato particular. Inclusive, la prueba de Merkle no requiere que el árbol esté completo, sino que se pueda acceder al fragmento de interés.
Verificar la integridad, una parte a la vez
La principal ventaja que se obtiene de aplicar árboles de Merkle a las cadenas de bloques es la capacidad de verificar la integridad de cualquier parte de la cadena, un bloque específico, una transacción en particular, sin que sea necesario descargar la cadena entera.
Como hemos visto, cada bloque de una blockchain es una estructura de datos. En el encabezado del bloque, junto a otros datos como la marca de tiempo, nonce, hash del bloque anterior, versión del bloque y dificultad actual, se encuentra alojado también el hash raíz del árbol de Merkle.
Gracias a este diseño de bloque, fueron proyectados los nodos de Verificación de Pago Simple (SPV) que aparecen en la sección 8 del whitepaper de Bitcoin. Los nodos SPV, o “clientes ligeros”, sólo descargan los encabezados de bloques de la cadena más larga (actualizada), y no la cadena completa de Bitcoin. Estos nodos verifican con otros nodos de la red que, efectivamente, los encabezados sobre los que están trabajando provienen de bloques de la cadena más larga. Hecho esto, el nodo SPV puede proceder con el análisis de una transacción de interés mediante la aplicación de la prueba de Merkle.
Teóricamente, los árboles de Merkle podrían ayudar a ahorrar espacio de almacenamiento en disco. Como el hash raíz se guarda en el encabezado del bloque, algunos bloques de la cadena, los que tienen más tiempo en ella, pueden llegar a “podarse” al eliminar las ramas del árbol que no participan en la prueba de Merkle.
Ethereum y demás aplicaciones
Aparte de Bitcoin, otras blockchains utilizan árboles de Merkle, esquemas similares o de mayor complejidad. Ethereum es una de esas cadenas, y emplea una versión compuesta por varios árboles conocida como Merkle Patricia Trie (MPT). El vocablo “trie” es prestado del idioma francés, y significa “clasificación/organización”. En computación es equivalente a usar la palabra árbol (tree).

Los árboles de Merkle juegan un rol vital en cuanto a la integridad y seguridad de las cadenas de bloques, y se emplean para la administración de código fuente de programas con métodos distribuidos de verificación de cambios como Git. El Sistema de Archivos InterPlanetario (IPFS) también hace uso de ellos.
IPFS puede llegar a ser una alternativa a Internet, ya que posee su propio sistema de nombres, IPNS, para direccionar el contenido que maneja. Esto puede considerarse una solución ideal para saltarse las prohibiciones en los casos donde las leyes locales impidan el acceso a ciertos contenidos de la web. Las páginas no accesibles podrían entonces ser duplicadas en IPFS, como sucedió en Cataluña en 2017, cuando los sitios de los partidarios independentistas fueron bloqueados por la Corte Suprema de Justicia.